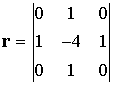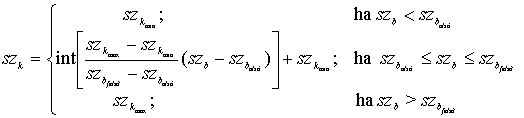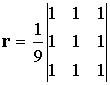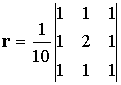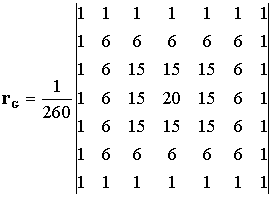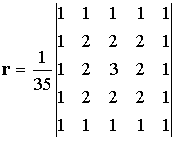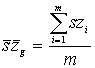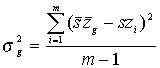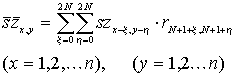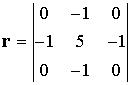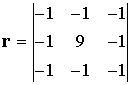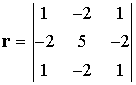Képfeldolgozás II
Ebben a részben tulajdonképpen folytatjuk a képfeldolgozással kapcsolatos ismereteink bővítését és megismerkedünk néhány gyakorlati képfeldolgozási módszerrel, ezen belül
- az élkiemeléssel,
- a hisztogram fogalmával, és a hisztogram transzformációval történő képfeldolgozással , és néhány
- lokális szűrési eljárással.
Gyakorlati képfeldolgozási módszerek
Az ismertetett matematikai alapok felhasználásával lehetőség nyílik arra, hogy a képekből kiemeljük az éleket, illetve a képek élességének illetve kontrasztosságának globális vagy helyi változtatására.
Élkiemelés
Egy korábbi pontban megismerkedtünk a kölcsönös tájékozás fogalmával és bemutattuk azt a módszert, mely segítségével a kapcsoló pontok parallaxis különbsége automatikusan, lineáris korreláció segítségével számítható. Nem szóltunk azonban arról hogyan választjuk ki a mintaállományt illetve a keresési állományt, hogyan biztosítható, hogy a korreláció megbízható eredményeket szolgáltasson, s egyben a keresési állományt lehetőleg kis területre korlátozzuk. A módszer, mellyel ezek a kérdések megoldhatók az élkiemelésen alapul. Még nagyobb az élkiemelés jelentősége, ha a kölcsönös tájékozást a kiemelt és a két képen megfelelőként azonosított élek alapján végezzük kétdimenziós korrelációval.
Hasonlóképpen fontos szerepet játszik az élkiemelés a számítógépes alakfelismerésben, amikor digitális ortofotó vagy szkennelt térkép szabályos entitásait (házak, utak, térképek esetében szimbólumok) kívánjuk automatikusan felismerni és a GIS objektummá alakítani.
Harmadik alkalmazási területként a digitális magasságmodell segítségével történő felületelemzést említjük, amikor az 'élkiemelés' tulajdonképpen az idomvonalak (hátvonalak, völgyvonalak) detektálását szolgálja. Az ismertetett módszer eredményeképpen megkapjuk azokat a helyeket ahol a képfüggvényen alkalmazott LoG operátor zérus eredményt ad. Az így nyert 'kép' azonban túl kontrasztos és rendszerint csak az élek helyével összefüggő műveletekre használható. Azt hogy miként használhatjuk a Laplace operátort kontrasztnövelésre a lokális szűrési módszerek között fogjuk tárgyalni.
Legegyszerűbben az élkiemelést az úgy nevezett második különbségek módszerével hajthatjuk végre.
Diszkretizáljuk kétdimenziós esetre a
skalár függvényre alkalmazott Laplace operátort olymódon, hogy a ![]() függvényt
helyettesítsük a kétdimenziós sz(x,y) szürkeségi érték függvénnyel, a
deriváltakat pedig a kérdéses pixelre vonatkozó differencia hányadosokkal.
Eljárásunk eredményeképpen az i,j pixelre vonatkozó második
szürkeségi érték különbség a következő képlettel írható fel:
függvényt
helyettesítsük a kétdimenziós sz(x,y) szürkeségi érték függvénnyel, a
deriváltakat pedig a kérdéses pixelre vonatkozó differencia hányadosokkal.
Eljárásunk eredményeképpen az i,j pixelre vonatkozó második
szürkeségi érték különbség a következő képlettel írható fel:
|
|
. |
Nem nehéz felismerni hogy a fenti eredményt úgy is megkaphatjuk, ha a diszkrét konvolúció kifejezésében az alábbi r mátrixot alkalmazzuk:
|
|
. |
Úgy is fogalmazhatunk, hogy ha a konvolúciót végrehajtjuk a szürkeségi érték függvényen a fenti r szűrő mátrixszal, úgy az eredményen az élek kiemelődnek.
A LoG operátor alkalmazása esetén, a szűrést és az
élkiemelést együtt végezzük. A szűrés ebben az esetben azt a célt szolgálja,
hogy a segítségével csak azokat az éleket válasszuk ki, melyek az adott feladat
szempontjából számításba jönnek. Így a kölcsönös tájékozáshoz távoli élek tehát
nagy szigma értékek szükségesek, míg a tájékozott képekben végrehajtott
parallaxis meghatározás kis szigmákat igényel. Nem szabad azonban
elfelejtenünk, hogy a ![]() növelése a szűrésre felhasznált mátrix dimenziójának
növekedésével jár, hisz a 3.49-es ábrán látható
görbe annál szélesebb és laposabb minél nagyobb
növelése a szűrésre felhasznált mátrix dimenziójának
növekedésével jár, hisz a 3.49-es ábrán látható
görbe annál szélesebb és laposabb minél nagyobb ![]() . A LoG
operátor ugyanis
. A LoG
operátor ugyanis ![]() értéknél veszi fel a 0 értéket.
értéknél veszi fel a 0 értéket.
Az operátort ábrázoló felület és az XY sík közötti köbtartalom egy negatív és egy pozitív részből áll, melyek összege zérus. Amikor a függvényt diszkretizáljuk (a pixel középpontok fölé eső ordinátákból álló négyzetes szimmetrikus mátrixszal helyettesítjük) gondoskodnunk kell arról hogy a kerekítéseket úgy végezzük, hogy a mátrix-ablak elemeinek összege zérust adjon.
A hisztogram fogalma, képfeldolgozás hisztogram transzformációval
Az sz szürkeségi értékek a szkennerekben egy pixel tárolására figyelembe vett bitek b számának, illetve a szenzor érzékenységének függvényében 0 és 2b-1 között a megvilágítás erősségével arányos egész szám értéket vesznek fel. Azt az analóg-digitális transzformációt, amely a szkennelés során keletkező feszültségeket intervallumokba rendezi és a feszültség intervallumokat a szürkeségi érték skálán elhelyezkedő egész számokhoz rendeli kvantálásnak nevezzük.
Ha egy síkbeli derékszögű koordináta rendszerben a vízszíntes tengelyre felrakjuk a kvantálás eredményeképpen nyerhető sz szürkeségi értékeket a 0 és 2b-1 határok között, a függőleges tengelyre pedig az adott szürkeségi értékű pixelek számának hányadosát az összes pixelek számával, úgy a szürkeségi értékek gyakorisági görbéjét, vagy idegen szóval hisztogramját nyerjük.
|
|
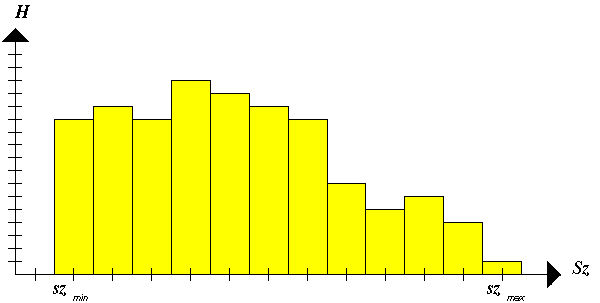
Egy egyszerű kisméretű hisztogramot a 3.50 ábrán mutatunk be, a h ordináta értékek a h = nsz / N kifejezésből számíthatók, ahol nsz a kérdéses szürkeségi értékű pixelek száma, N pedig az összes pixel száma.
Az eredeti kép hisztogramjának módosításával, illetve az eredeti szürkeségi érték skála megváltoztatásával, ami ugyancsak a feldolgozott kép hisztogramjának megváltozásával jár együtt, csökkenteni tudjuk a helytelen megvilágításból eredő hibákat, valamint a képek túlzott kontraszt szegénységét. Olyan gyakorlati esetekben is szükségünk lehet a hisztogramok transzformációjára, amikor a rendelkezésünkre álló megjelenítő eszköz (grafikus kártya) képtelen a képekben adott tónusgazdagságot vagy színszámot visszaadni s ezért a szürkeségi érték vagy színtartományt redukálni kell. Sok hisztogram transzformációs módszert beépített függvényként alkalmaznak a raszteres GIS szoftverek, ezért célszerű ha megismerkedünk néhány eljárás alapelvével.
Jelölje a bemenő szürkeségi értékek halmazát Szb, a
transzformáció eredményeképpen kapott szürkeségi érték halmazt pedig Szk. Jelöljük az
eredeti és transzformált halmazok legkisebb és legnagyobb értékeit szbmin, szkmin illetve szbmax, szkmax-al. Mivel a
transzformáció során nem feltétlelenül az egész bemenő intervallumot kívánjuk
transzformálni jelöljük a bemenő jel transzformációban figyelembe veendő alsó
illetve felső határát szbalsó ![]() szbmin és szbfelső
szbmin és szbfelső ![]() szbmax -al.
szbmax -al.
A gyakori, szakaszonkénti lineáris transzformációt az alábbi kifejezéssel hajtjuk végre:
|
|
. |
A kifejezésből látható, hogy a transzformációhoz meg kell adnunk mind szbalsó és szbfelső, mind pedig szkmin és szkmax értékeit.
A vázolt módszerrel kétféleképpen is módosíthatjuk a szürkeségi értékeket. Ha szbalsó>szbmin és/vagy szbfelső<szbmax akkor sávszűkítésről beszélünk, akkor alkalmazhatjuk, ha olyan szürkeségi értékeink vannak a sáv szélén, melyek nem jeleníthetők meg, vagy ha a sáv szélen található szürkeségi értékek elhagyása csak érdektelen területeken csökkenti a kontrasztot, globálisan viszont erősíti a képpontok különbségét tehát növeli a kontrasztot. Ez utóbbi megállapítás persze csak akkor igaz, ha a bemenő és kimenő kép szürkeségi intervalluma azonos marad.
Ha az eredeti kép szürkeségi értéktartománya nem tölti ki a lehetséges intervallumot a kimenő képet a lineáris transzformációval széthúzhatjuk a lehetséges szürkeségi érték tartományra, ami egyfelől azt fogja eredményezni, hogy a kontraszt globálisan növekszik, másfelöl, hogy a kimenő hisztogramban lukak keletkeznek.
Lineáris transzformálás helyett a transzformációra más függvények is alkalmazhatók. Ha a függvényt f(szb)-el jelöljük, úgy a transzformált szürkeségi értékeket az
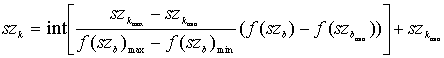
kifejezésből nyerjük.
Amint már említettük, a két fenti kifejezésben
a kimenő szürkeségi értékek maximális és minimális értéke szabadon választható
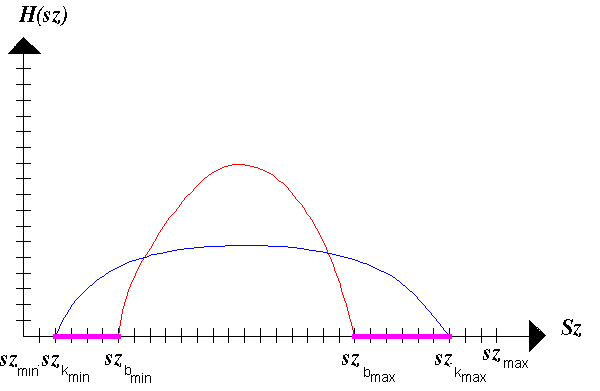
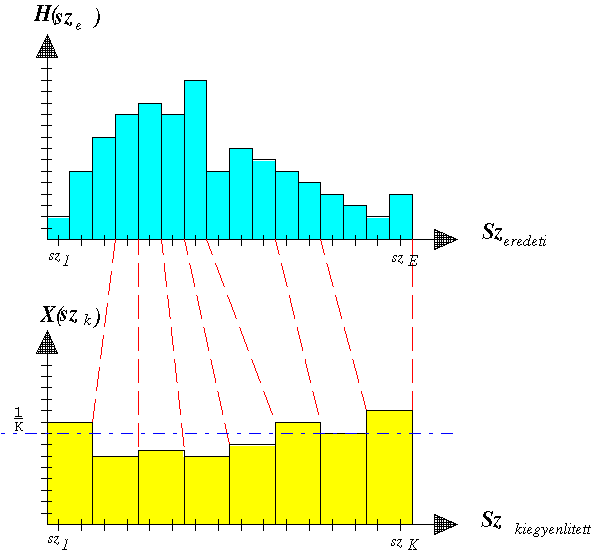
paraméterként jelentkezik. Ha ezeket a paramétereket a 3.51 ábrán felvázolt
módon úgy választjuk meg, hogy a bemenő hisztogram szélességét egy s
skalárral megnyújtjuk, és egyben gondoskodunk arról, hogy a kimenő hisztogramm
szélső értékeinek távolságai a lehetséges szürkeségi értékek határoló
értékeitől úgy arányoljanak egymáshoz mint a bemenő hisztogram szélső értékei
és a kimenőhisztogram szélső értékei közötti intervallumok, úgy
olyan módszert kapunk, mely alkalmas az egyenlőtlen háttér megvilágítás
kiegyenlítésére.
A transzformált szürkeségi értékeket az alábbi
kifejezésből nyerjük: 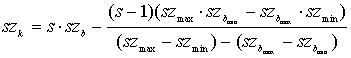
|
|
|
Megfigyelhetjük, hogy az eddig alkalmazott szürkeségi érték transzformációk során a hisztogram ordinátákat nem vettük figyelembe a számításoknál. A következő transzformáció-típus az úgy nevezett hisztogram kiegyenlítés már számol ezekkel a mennyiségekkel is.
Az eljárás egyik célja az, hogy utólagosan finomítsa a gyakori szürkeségi értékeknek megfelelő kvantálást, míg a ritkább szürkeségi értékű képpontok szürkeségi osztályait csökkentse, s ezzel elérje, hogy a kimenő hisztogram ordinátái egy konstans egyeneshez közelítsenek. Másik célként azt jelölhetjük meg, hogy normalizálni akarjuk valamilyen célból a fényképet. Ilyen cél lehet például, ha az átfedő kép pár képei különböző megvilágítási viszonyok mellett készültek. Ebben az esetben a közös feldolgozás minőségét jelentősen javíthatja, ha az egyik kép hisztogramját a másik kép hisztogramjára transzformáljuk.
Jelölje az eredeti hisztogramm ordinátáit ![]() , a
kiegyenlített hisztogramét pedig
, a
kiegyenlített hisztogramét pedig ![]() , akkor a hisztogram
alapértelmezéséből következik, hogy
, akkor a hisztogram
alapértelmezéséből következik, hogy
|
|
. |
Az átalakítás feladata abban rejlik, hogy a kiegyenlített hisztogram az
eredetinek valamilyen függvénye legyen s egyben lépésenként kielégítse
az alábbi összefüggést:
|
|
. |
Az előbbi kifejezés direkt megoldását nehezíti, hogy mn explicit
kifejezése általában nehézségekkel jár, ezért a direkt megoldás helyett
rendszerint iterációt alkalmaznak.
A 3.52 ábra példáján azt tételeztük fel, hogy a kiegyenlített hisztogramban a szürkeségi érték osztályok száma éppen az eredeti szürkeségosztályok számának fele,
a számítást úgy végeztük, hogy sorra kiszámítottuk azokat az mn-eket, melyekre az alábbi egyenlőtlenség fennáll:
Az mn-ek ismeretében
aztán kiszámíthatók az egyenletet kielégítő Amint a 3.52 ábrából is látható az eredményként kapott hisztogram nem teljesen egyenletes ami azzal magyarázható, hogy az egyenlet csak akkor oldható meg pontosan, ha az eredeti szürkeségi osztályokat tovább bontjuk és ugyanahhoz a szürkeségi osztályhoz tartozó pixelekhez különböző szürkeségi értékeket rendelünk a kiegyenlített hisztogramban. Nem igényel részletes magyarázatot, hogy ezt az átcsoportosítást csak akkor tudjuk visszavezetni a konkrét pixelekre ha figyelembe vesszük a szomszédos pixelek eredeti szürkeségi értékeit is. |
|
Lokális szűrési eljárások
A lokális szűrési eljárások két főcsoportra oszthatók. Az első csoport simítja a képeket, csökkenti a kontrasztot, a második csoport éppen ellenkezőleg a kontraszt kiemelésére szolgál.
A simító eljárások lineáris és nem lineáris alcsoportokra oszthatók.
A lineáris módszerek közvetlenül alkalmazzák a diszkrét konvolúciót. A módszerek közötti különbség abban van, hogy milyen az r mátrix.
A simítás akkor a legteljesebb ha
|
|
. |
Nem nehéz észrevenni, hogy a fenti mátrixszal történő szűrés eredményeképpen minden képpont szürkeségi értéke a szűrés után egyenlő lesz a kérdéses pont és a szomszédos pontok szürkeségi értékeinek számtani közepével. Problémaként merülhet fel, hogy miként értelmezzük ezt és a további eljárásokat a szélső pixelek esetében.
Legegyszerűbb az az eljárás amikor a szűrő dimenziójának megfelelően csökkentik a szűrt kép dimenzióját: 3x3-as szűrő esetén az első és utolsó sorral és oszloppal, 5x5-ös szűrő esetén két-két sorral és oszloppal stb.
Gyakran alkalmazzák azt a módszert, amikor az érintett szélső pixelek szürkeségi értékeit változatlanul hagyják.
Végül, alkalmazhatják a diszkrét konvolúció felírásakor elfogadott feltételt is, hogy a transzformálandó kép dimenzióját az érintett sorok és oszlopok tükrözésével megnövelik.
Az egyszerű számtani közép helyett a szűrést végezhetjük súlyozott számtani középképzéssel is például az alábbi szűrő mátrix alkalmazásával:
|
|
. |
A normáleloszlás sűrűség függvénye, mely egyszerű szemlélet alapján is beláthatóan, diszkretizálás után alkalmas lehet a diszkrét képelemeken végrehajtott szűrési funkcióra, a binomiális eloszlás felhasználásával az alábbi 7x7-es szűrőmátrixszal közelíthető:
|
|
. |
A nagyméretű szűrőmátrixok alkalmazása azonban a futásidő szempontjából nem előnyös, ezért a szélesebb tartományra eső súlyozás szüksége esetén inkább kisebb szűrőmátrixszal végeznek többszöri szűrést. Igazolható ugyanis [11], hogyha az egyenletes súlyozású szűrőmátrixot egymásután háromszor végigfuttatjuk a képen (természetesen az eredeti képen csak egyszer, utána az egyszer szűrt képen, utána pedig a kétszer szűrt képen), úgy ez egyenértékű azzal mintha az alábbi 5x5-ös mátrixszal végeznénk a szűrést:
|
|
. |
A lineáris szűrési eljárásokat tulajdonképpen azért nevezzük lineárisnak, mivel a térben végrehajtott konvolúció a frekvencia tartományban a műveletben résztvevő függvények Furier transzformáltjai közötti szorzásra egyszerűsödik. A műveleteket a frekvencia tartományban végrehajtva szemléletessé válik, hogy a simító szűrők alúláteresztő szűrők, mivel csak az alacsonyabb térfrekvenciájú komponenseket eresztik át, a magasabbakat elnyomják.
A gyakorlatban igen eredményesen alkalmaznak olyan szűrő eljárásokat, melyek nem tekinthetők konvolúciónak, s ezért nem vihetők át lineáris műveletek formájában a frekvencia tartományba. Ezeket az eljárásokat nem lineáris szűrő eljárásoknak nevezzük.
Első nem lineáris eljárásként ismerkedjünk meg a küszöb alatti középérték képzéssel. Az eljárás szavakkal úgy fogalmazható meg, hogy az előzőekben ismertetett szűrő módszer nyújtotta középértéket csak akkor fogadjuk el a pixel új értékének, ha az eredeti szürkeségi értéktől kisebb mértékben különbözik (azaz az eltérés abszolút értéke kisebb) mint az előre megadott T küszöb érték. Ha ez a feltétel nem teljesül, úgy a vizsgált pixel eredeti szürkeségi értéke az eljárás során változatlan marad. A módszer segítségével a T érték függvényében többé vagy kevésbé biztosítani tudjuk azt, hogy az élek a simítás ellenére is fennmaradjanak. A helyes T érték megválasztása két értelemben is feladatfüggő: függ a szűrendő kép textúrájától s a megoldandó feladattól.
A mediánszűrés esetén az alkalmazott ablakkal (3x3, 5x5) egymásután lefedjük az eredeti kép valamennyi pixelét (a szélső pixelekkel kapcsolatos problémák lehetséges megoldásairól a lineáris szűrésekkel kapcsolatban már szóltunk). Minden szűrőhelyzetben a lefedett képpixelek szürkeségi értékeit sorbaállítjuk és a helyzet középső pixelének szűrt értékét egyenlővé tesszük a nagyság szerint középső szürkeségi értékkel. Ha valamely szűrő helyzetben a különböző szürkeségi értékek száma páros, úgy a középre szimmetrikus két szomszédos szürkeségi érték középértékét tekintik médiánnak. A módszer alkalmazása kis ablakok esetén nem befolyásolja a jelentősebb élek (vonalak) leképződését a szűrt képen.
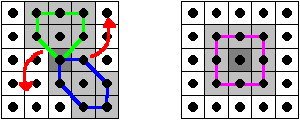
A Nagao féle szürés rendszerint 5x5-ös ablakkal dolgozik. Az ablakot a korábbi eljárásokhoz hasonlóan végigtoljuk a bemenő kép pixelein. Minden ablak helyzetben a középső pixelnek megfelelő pixel szürkeségi értékét a szűrt képen egyenlővé teszik az ablak által lefedett bemenő pixelek egy részhalmaza szürkeségi értékeinek számtani közepével. 5x5-ös ablak esetén a 3.53 ábra szerinti nyolc darab egyenként 7 pixelt tartalmazó, széleiken átfedő szabálytalan és egy középponti 9 pixeles részhalmaz vizsgálatára kerül sor.
|
Abból a részhalmazból számolják a középértéket, amely szürkeségi értékeinek varianciája a legkisebb (legyen a részhalmazban található pixelek száma m, a g.-ik részhalmaz szürkeségi értékeinek számtani közepe
|
|
||||||||||||
A módszer alapelvéből következik, hogy a pixelek közötti jelentős szürkeségi érték különbségek, melyek élekre utalnak, nem folynak bele a simítási folyamatba.
Bár a hétköznapi szóhasználat szűrés alatt a simítást vagy az egyenlőtlenségek kiküszöbölését érti, amint láttuk ez a szűrés típus a Furier transzformáción alapuló rádiótechnikai analógiával csak az alul áteresztő szűrést valósítja meg. A felül áteresztő szűrésnek az a specifikus válfaja, mely az alacsonyabb frekvenciákat nem oltja ki teljesen, hanem csak csökkenti szolgál a képfeldolgozásban a kontraszt erősítésére.
A Laplace illetve LoG operátorok alkalmazásával kapcsolatban megismerkedtünk az élkiemelés fogalmával, de azt mondtuk, hogy az így kiemelt kép túl kontrasztos és csak a kérdéses (a LoG esetén megfelelő térgyakoriságú) élek detektálására alkalmas.
A Laplace operátort azonban felhasználhatjuk a kontraszt növelésére is, ha kivonjuk az eredeti szürkeségi értékből:
|
|
. |
A c egy kísérletileg meghatározandó konstans. A fenti szűrés konvolúciós formában is megadható. Emlékeztetőül írjuk fel még egyszer a diszkrét konvolúció képletét:
|
|
. |
Az r2N+1,2N+1 mátrix N=1 és c=1 esetén:
|
|
. |
A c változtatásával növelhetjük illetve csökkenthetjük a kontrasztosságot. Természetesen bármilyen c-t is alkalmazunk az eredményül kapott kép kontrasztosabb lesz mint az eredeti kép.
A LoG operátort gyakorlati szempontból nem célszerű
ennél a szűrésnél a Laplace operátor helyett alkalmazni, mivel a ![]() függvényében
3x3-asnál jóval nagyobb szűrő mátrix kell a közelítéséhez. Az irodalomban
azonban számtalan 3x3-as mátrixszal találkozunk a felüláteresztő szűrőkben,
példaképpen a [12] alapján még bemutatunk kettőt:
függvényében
3x3-asnál jóval nagyobb szűrő mátrix kell a közelítéséhez. Az irodalomban
azonban számtalan 3x3-as mátrixszal találkozunk a felüláteresztő szűrőkben,
példaképpen a [12] alapján még bemutatunk kettőt:
|
|
, illetve |
|
. |
ˇ a következő részben megkezdjük a távérzékelés tárgyalását
ˇ esetleg visszatérhet az előző részhez
ˇ illetve a tartalomjegyzékhez
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc